Problem 4. Let  be an integer. Let  be positive real numbers such that

.

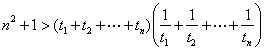Show that   are side lengths of a triangle for all  with  .

Problem 5. In a convex quadrilateral  the diagonal  bisects neither the angle  not the angle .

The point  lies inside  and satisfies

Prove that  is a cyclic quadrilateral if and only if .

Problem 6. We call a positive integer alternating if every two consecutive digits in its decimal representation

are of different parity.  Find all positive integers  such that  has a multiple which is alternating.

                                                                                                                                                   Duration of exam: 4 hours 30 minutes.

                                                                                                                                                   Each problem is worth 7 marks.