|
45th
INTERNATIONAL MATHEMATICAL OLYMPIAD
IMO 2004
HELLAS |

|
|
|
|
Day: |
1 |
Country Code: |
66 |
Country Abbr.: |
SIN |
Language: |
English |
|
|
| |
|
|
|
|
|
|
|
|
Problem 1. Let
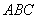 be an acute-angled triangle with
be an acute-angled triangle with
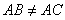 . The circle with diameter
. The circle with diameter
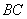 intersects
intersects
the sides
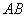 and
and 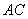 at
at 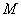 and
and 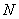 , respectively. Denote by
, respectively. Denote by
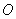 the midpoint of the side
the midpoint of the side
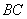 . The
. The
bisectors of the angles
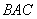 and
and 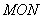 intersect at
intersect at 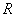 . Prove that the circumcircles of the triangles
. Prove that the circumcircles of the triangles
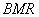
and
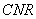 have a common point lying on the side
have a common point lying on the side
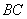 .
.
Problem 2. Find all polynomials
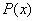 with real coefficients which satisfy the equality
with real coefficients which satisfy the equality
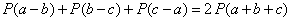
for all real numbers
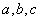 such that
such that 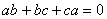 .
.
Problem 3. Define a
hook to be a figure made up of six unit squares
as shown in the diagram
or any of the figures
obtained by applying rotations and reflections to this figure.
Determine all
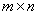 rectangles that can be covered with hooks so that
rectangles that can be covered with hooks so that
·
the rectangle is covered without
gaps and without overlaps;
·
no part of a hook covers area
outside the rectangle.
Duration of exam: 4 hours 30 minutes.
Each problem is worth 7 marks.
